Ένας πρωταθλητής του γκολφ μπορεί να στέλνει το μπαλάκι σε απόσταση ακριβώς 3, 5, 7 ή 11 μέτρα. Δυστυχώς με τις υπόλοιπες αποστάσεις δεν είναι καθόλου σίγουρος, γι αυτό αποφεύγει να τις επιχειρήσει. Αυτό όμως δεν αποτελεί σοβαρό πρόβλημα γιατί ακόμα και αν το μπαλάκι του ξεπεράσει την τρύπα, μπορεί πάντα να το χτυπήσει προς τα πίσω, κατά τις γνωστές του αποστάσεις, μέχρι να καταφέρει να το βάλει μέσα.
Σε κάποιον αγώνα βρέθηκε το μπαλάκι του σε απόσταση 20 μέτρων από την τρύπα. Επειδή είναι επίσης και πολύ καλός στα μαθηματικά, βρήκε τον τρόπο να βάλει το μπαλάκι στην τρύπα με τις ελάχιστες δυνατές προσπάθειες, χτυπώντας μόνο τις γνωστές του αποστάσεις. Πόσες προσπάθειες χρειάστηκε;
Μετρήστε την ευφυΐα σας!
Πόσο έξυπνοι είστε; Βρείτε την απάντηση σε αυτό το ερώτημα λύνοντας μερικούς από τους καλύτερους γρίφους αυτού του blog, συγκεντρωμένους σε μία εφαρμογή Android. Κατεβάστε την εφαρμογή από το Google Play Store.
Τετάρτη 3 Μαρτίου 2010
Έμπνευσης - Συσκευές μέτρησης χρόνου (**)
Το ηλιακό ρολόι είναι η συσκευή μέτρησης του χρόνου με τα λιγότερα κινούμενα μέρη. Ποια είναι η συσκευή μέτρησης χρόνου με τα περισσότερα κινούμενα μέρη;
Κατηγορία Γρίφου:
.Λυμένοι,
2* Εύκολος,
Έμπνευσης
Έμπνευσης - Δύο τρένα (*)
Ένα τρένο ξεκινάει στις 6 το πρωί από Αθήνα με κατεύθυνση τη Θεσσαλονίκη. Κινείται με ταχύτητα 120 χιλιόμετρα την ώρα. Η απόσταση Αθήνας - Θεσσαλονίκης είναι 515 χιλιόμετρα.
Ένα δεύτερο τρένο ξεκινάει την ίδια μέρα στις 8 το πρωί από Θεσσαλονίκη με κατεύθυνση την Αθήνα. Κινείται με ταχύτητα 150 χιλιόμετρα την ώρα.
Όταν θα συναντηθούν, ποιο από τα δύο τρένα θα βρίσκεται πιο κοντά στην Αθήνα;
Ένα δεύτερο τρένο ξεκινάει την ίδια μέρα στις 8 το πρωί από Θεσσαλονίκη με κατεύθυνση την Αθήνα. Κινείται με ταχύτητα 150 χιλιόμετρα την ώρα.
Όταν θα συναντηθούν, ποιο από τα δύο τρένα θα βρίσκεται πιο κοντά στην Αθήνα;
Κατηγορία Γρίφου:
.Λυμένοι,
1* Πολύ εύκολος,
Έμπνευσης
Λογικής - Πραγματικό μέντιουμ (***)
Επιτέλους, μετά από χρόνια ερευνών, βρέθηκε ένα μέντιουμ που προέβλεπε σωστά το μέλλον με ποσοστό επιτυχίας 100%. Δεχόταν έναν πελάτη στο σπίτι του, αυτός του έκανε μια ερώτηση για το μέλλον και το μέντιουμ απαντούσε μόνο με ναι ή όχι. Απαραίτητη προϋπόθεση για να λειτουργήσει σωστά η πρόβλεψη ήταν ο πελάτης να μην μπορεί να επηρεάσει το μέλλον ανάλογα με την απάντηση του μέντιουμ. Παρόλα αυτά ένας πελάτης κατάφερε να του κάνει μια ερώτηση όπου το μέντιουμ προέβλεψε το μέλλον λανθασμένα. Τι το ρώτησε;
Κατηγορία Γρίφου:
.Λυμένοι,
3* Μέτριος,
Λογικής
Λογικής - Πόσοι πήραν μπαλόνι; (**)
Σε μια γιορτή του σχολείου, η δασκάλα ζήτησε από 10 παιδιά να παίξουν ένα παιχνίδι. Τους είπε να κλείσουν τα μάτια και φόρεσε στον καθένα τους είτε ένα κόκκινο είτε ένα άσπρο καπέλο. Μετά τους είπε να ανοίξουν τα μάτια τους και να δουν τα καπέλα που φοράνε τα υπόλοιπα παιδιά.
Όποιο παιδάκι έβλεπε τέσσερα ή περισσότερα κόκκινα καπέλα θα έπαιρνε δώρο ένα μπαλόνι. Στο τέλος του παιχνιδιού ένα παιδάκι ζήλεψε που κάποιο άλλο πήρε μπαλόνι ενώ αυτό όχι. Πόσα πήραν μπαλόνι;
Όποιο παιδάκι έβλεπε τέσσερα ή περισσότερα κόκκινα καπέλα θα έπαιρνε δώρο ένα μπαλόνι. Στο τέλος του παιχνιδιού ένα παιδάκι ζήλεψε που κάποιο άλλο πήρε μπαλόνι ενώ αυτό όχι. Πόσα πήραν μπαλόνι;
Κατηγορία Γρίφου:
.Λυμένοι,
2* Εύκολος,
Λογικής
Ανάλυσης - Κυκλική αλυσίδα (***)
Έχουμε οκτώ κομμάτια μιας αλυσίδας που αποτελούνται από επτά κρίκους το καθένα. Οι ακριανοί κρίκοι του κάθε τμήματος είναι κλειστοί. Θέλουμε να ενώσουμε και τα οκτώ τμήματα και να φτιάξουμε μια μεγάλη κυκλική αλυσίδα (οι άκρες της να ενώνονται).
Ένας τεχνίτης αναλαμβάνει να ανοίξει και να κλείσει όσους κρίκους του πούμε με κόστος 1 ευρώ ανά κρίκο (άνοιγμα - πέρασμα - κλείσιμο). Ποιο είναι το ελάχιστο κόστος που απαιτείται για να φτιάξουμε την αλυσίδα και ποιους κρίκους θα ζητήσουμε να μας ανοίξει;
Ένας τεχνίτης αναλαμβάνει να ανοίξει και να κλείσει όσους κρίκους του πούμε με κόστος 1 ευρώ ανά κρίκο (άνοιγμα - πέρασμα - κλείσιμο). Ποιο είναι το ελάχιστο κόστος που απαιτείται για να φτιάξουμε την αλυσίδα και ποιους κρίκους θα ζητήσουμε να μας ανοίξει;
Κατηγορία Γρίφου:
.Λυμένοι,
3* Μέτριος,
Ανάλυσης
Έμπνευσης - Διαβίβαση μηνύματος (***)
Οκτώ φίλοι έχουν πάει να παρακολουθήσουν μια συναυλία. Ξαφνικά ο ένας από αυτούς θέλει να διαβιβάσει επειγόντως ένα μήνυμα σε όλους τους υπόλοιπους. Λόγω του θορύβου που επικρατεί στο χώρο πρέπει να φωνάξει το μήνυμα στο αυτί ενός φίλου του και θα το ακούσει μόνο αυτός.
Αν το μήνυμα απαιτεί 10 δευτερόλεπτα για να διαβιβαστεί από φίλο σε φίλο, ποιος είναι ο ελάχιστος χρόνος που απαιτείται για να το λάβουν και οι οκτώ φίλοι;
Αν το μήνυμα απαιτεί 10 δευτερόλεπτα για να διαβιβαστεί από φίλο σε φίλο, ποιος είναι ο ελάχιστος χρόνος που απαιτείται για να το λάβουν και οι οκτώ φίλοι;
Κατηγορία Γρίφου:
.Λυμένοι,
3* Μέτριος,
Έμπνευσης
Έμπνευσης - Μισό δοχείο με νερό (****)
Έχουμε ένα διαφανές δοχείο ακανόνιστου σχήματος και μια πηγή με άφθονο τρεχούμενο νερό. Με ποιο τρόπο μπορούμε να γεμίσουμε το δοχείο μέχρι τη μέση της χωρητικότητάς του με νερό; Δεν έχουμε στη διάθεσή μας κανένα όργανο μέτρησης.
Κατηγορία Γρίφου:
.Λυμένοι,
4* Δύσκολος,
Έμπνευσης
Υπολογισμού - Δίπλωμα χαρτιού (**)
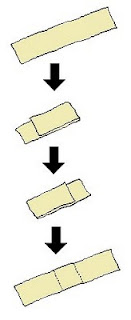
Ο Κωστάκης έχει πάνω στο γραφείο του μία λωρίδα χαρτιού και προσπαθεί να τη διπλώσει στη μέση. Σηκώνει το δεξί άκρο της, το τσακίζει σε κάποιο σημείο που του φάνηκε κεντρικό και το διπλώνει πάνω στο αριστερό άκρο. Βλέπει όμως πως από τα αριστερά περισσεύουν 10 εκατοστά χαρτιού. Ξανανοίγει το χαρτί και πιάνει το αριστερό άκρο το τσακίζει σε ένα διαφορετικό σημείο και το διπλώνει πάνω στο δεξί άκρο. Όμως πάλι περισσεύουν 10 εκατοστά, αυτή τη φορά από τη δεξιά πλευρά του χαρτιού. Απογοητευμένος απλώνει τη λωρίδα χαρτιού στο γραφείο του που τώρα έχει πάνω της τα ίχνη από δύο τσακίσεις. Πόσα εκατοστά απέχουν αυτές οι δύο τσακίσεις μεταξύ τους;
Κατηγορία Γρίφου:
.Λυμένοι,
2* Εύκολος,
Υπολογισμού
Υπολογισμού - Υπολογισμός ψηφίων (2) (***)
Συμβολίζουμε έναν τετραψήφιο αριθμό σαν ΑΒΓΔ που σημαίνει πως Α είναι οι χιλιάδες του, Β οι εκατοντάδες του, Γ οι δεκάδες του και Δ οι μονάδες του.
Βρείτε τα Α,Β,Γ,Δ που επαληθεύουν την ισότητα ΑΒΓΔ = 4 * ΔΓΒΑ
Βρείτε τα Α,Β,Γ,Δ που επαληθεύουν την ισότητα ΑΒΓΔ = 4 * ΔΓΒΑ
Κατηγορία Γρίφου:
.Λυμένοι,
3* Μέτριος,
Υπολογισμού
Υπολογισμού - Διαδρομή μυρμηγκιού (****)
Ένα μυρμήγκι έχει μπει μέσα σε ένα άδειο και κλειστό χαρτοκιβώτιο με διαστάσεις 40x30x20 εκατοστά. Βρίσκεται ακριβώς στη μία κορυφή του κουτιού και θέλει να περπατήσει μέχρι τη διαμετρικά απέναντι κορυφή, όπως φαίνεται στο σχήμα.
Ποιο είναι το μήκος της ελάχιστης διαδρομής που μπορεί να ακολουθήσει; Προσοχή γιατί υπάρχουν αρκετές επιλογές που δίνουν διαφορετικά μήκη διαδρομών.
Κατηγορία Γρίφου:
.Λυμένοι,
4* Δύσκολος,
Υπολογισμού
Εγγραφή σε:
Αναρτήσεις (Atom)